4.2        OLCR measurement of the complex impulse response

4.2.4       Propagation in dielectric materials

b)   Dielectric material with dispersion

We treat now the case of propagating waves in a dispersive dielectric material, where the second order of development of b is required (D_n of equation (4-20) is not null). We again superpose two versions of the original wave that have traveled in different materials over different distances. For clarity, the first wave is assumed to have traveled through vacuum over a distance z₁. The correspondent electrical field E₁ is then simply

where t₁ = z₁/c₀. Then, the second wave is assumed to have traveled in a dielectric media of refractive index n(n) over a physical distance z₂ (assumed positive). The expression of the electric field E₂ includes the dispersion coefficient D_n of the material through the propagation constant b(n) developed at the second order

The propagation time t₂ is defined as 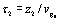. Thus, the interference intensity signal I(z₁,z₂) is given by

where the modified coherence function 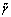is found to be

We introduce a variables change f = n-n₀ and then the 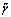takes the form

where u_D is the Fourier transform of U_D = exp(-ipD_n,0f²) and

The following relations has been used to obtain the Fourier transform of U_D

where TF means "the Fourier transform of". Finally

The function u_D in equation (4-31) also describes the pulse broadening in dispersive dielectric materials [4-7]. As it can be seen from equation (4-33), the dispersion greatly modifies the interference response. For OLCR set-ups that operate at 1500 nm, the fiber dispersion coefficient is not negligible. It is necessary to compensate the dispersion produced by the fiber section between P_te and P_t (Fig. 4-5). The function u_D(t) can be obtained from D_n and then, a deconvolution is possible by dividing S(n) by U_D(n) in the frequency domain. Experimental measurement of D_n can be obtained with two OLCR interferogram responses for a cleaved fiber of different length. A complete dispersion compensation algorithm based on a similar formalism can be found in the work of A. Kohlhaas [4-8] for multiple localized reflectors in the test arm.

The case of two wave components traveling in two different dispersive dielectric materials gives similar results. The modified coherence function 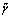can also be expressed in the following form : exp(-ij)×g(t)*u₂(t). The factor j is identical to the case of non-dispersive materials (a)). The function u₂(t) is similar to u_D(t) defined in equation (4-31) but with 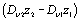instead of and . This indicates another way to compensate the dispersion effect in all-fiber OLCR, that is by using in the reference arm a piece of fiber with bigger dispersion coefficient or by using in the test arm a piece of fiber with opposite sign dispersion coefficient. The total effect has to cancel the term .
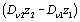